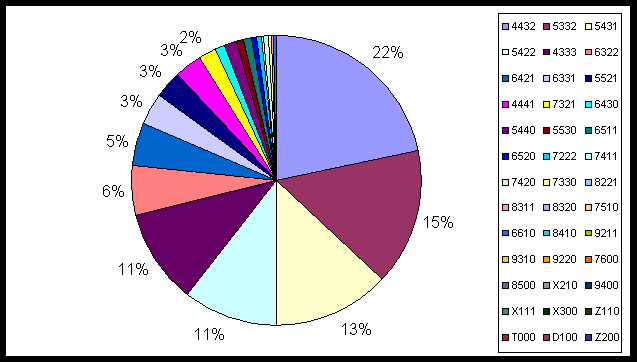
Il y a 39 mains de base au bridge réparties en quatre types :
1. Unicolore : T000 ; D100 ; Z200 ; Z110 ; X300 ; X210 ; X111 ;9310 ; 9220 ; 9211 ; 8320 ; 8311 ; 8221 ; 7330 ; 7321 ; 7222 ; 6331 ; 6322
2. Bicolore : 9400 ; 8500 ; 8410 ; 7600 ; 7510 ; 7420 ; 7411 ; 6610 ; 6520 6511 ; 6430 ; 6421 ; 5530 ; 5521 ; 5431 ; 5422
3. Tricolore : 5440, 4441
4. Régulier : 5332 ; 4432 ; 4333
( T = treize ; D = douze ; Z = onze ; X = dix ).
Ces mains se répartissent comme suit :

Les fréquences observées sur un échantillon aléatoire de 6 milliards (6 x 109) de donnes sont les suivantes (en %):
4432 : 0,21554133 5332 : 0,15494777 5431 : 0,12925879
5422 : 0,10576012 4333 : 0,10545009 6322 : 0,05653297
6421 : 0,04707967 6331 : 0,03457042 5521 : 0,03171976
4441 : 0,02997719 7321 : 0,01875876 6430 : 0,01322797
5440 : 0,01243268 5530 : 0,00897641 6511 : 0,00703236
6520 : 0,00649547 7222 : 0,00514349 7411 : 0,00392261
7420 : 0,00360978 7330 : 0,00263072 8221 : 0,00191943
8311 : 0,00120427 8320 : 0,00107617 7510 : 0,00107057
6610 : 0,00072229 8410 : 0,00045761 9211 : 0,00017832
9310 : 0,00010351 9220 : 0,00008734 7600 : 0,00005075
8500 : 0,00003142 X210 : 0,00001098 9400 : 0,00000966
X111 : 0,00000395 X300 : 0,00000131 Z110 : 0,00000039
Z200 : 0 D100 : 0 T000 : 0
On voit que trois mains (4432 ; 5332 et 5431) constituent la moitié des jeux et qu’on dépasse les trois quarts en en ajoutant 3 autres (5422 ; 4333 et 6322).
La représentation des quatre types est :
Unicolore : 12,217 %
Bicolore : 35,940 %
Tricolore : 04,238 %
Régulier : 47,605 %
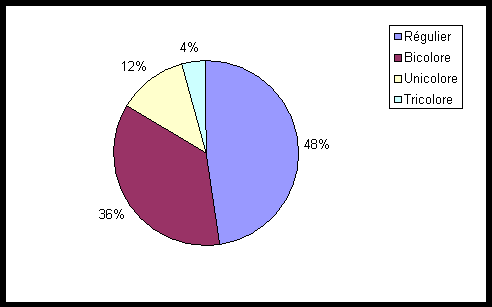
Types des mains dans une ligne
La valeur d’une main dépend de celle du partenaire, la combinaison des deux donne la main de la ligne. Sa détermination est plus complexe car les deux profils ne mains ne
sont pas indépendants. Avec 6321 à PCKT, Sud a beaucoup plus de chances de trouver 6 trèfles que 6 piques chez son partenaire. Nous avons estimé
ces probabilités à partir de l’échantillon de six milliards de donnes aléatoires qui fournit des limites de confiance élevées.
Les couleurs seront maintenant appariées, par exemple 5431 – 2335 signifie que les quatre couleurs sont : 5-2 ; 4-3 ; 3-3 ; 1-5.
Il y a donc beaucoup plus que 39 mains possibles pour le partenaire puisque l’ordre n’est plus strictement décroissant.. Il y en en théorie 24 ordres pour 4
couleurs (4 !), soit 39 x 24 = 936. Etant donné les ex-aequo, ce nombre théorique est en fait de 650 (24 x 11 + 12 x 12 + 4 x 5) et le nombre réellement
observé est de 519, ce qui signifie que 41 positions n’apparaissent jamais, soit parce qu’elles sont plus que rarissimes (e.g. T000 ; D100 et Z200
qui n’apparaissent jamais dans l’échantillon de 6x109 donnes), soit parce qu’elles sont incompatibles avec la main du partenaire (e.g. 7321 en face de 7222).
Voici, en fonction des quatre types de base, les effectifs des mains de ligne (Sud en lignes et Nord en colonnes) :
|
Unicolore |
Bicolore |
Tricolore |
Régulier |
Total |
|
|
Unicolore |
98 198 548 |
289 636 462 |
34 773 151 |
310 091 044 |
732 699 205 |
|
Bicolore |
288 853 821 |
796 038 870 |
89 855 093 |
981 406 040 |
2 156 153 824 |
|
Tricolore |
34 700 115 |
89 239 297 |
10 074 217 |
120 118 649 |
254 132 278 |
|
Régulier |
311 580 087 |
981 658 491 |
119 756 723 |
1 444 019 392 |
2 857 014 693 |
|
Total |
733 332 571 |
2 156 573120 |
254 459 184 |
2 855 635 125 |
6 000 000 000 |
Le tableau n’est pas symétrique car il n’y a aucune raison pour qu’un tirage aléatoire donne exactement autant de mains unicolores-régulières que de main régulières-unicolores par exemple.
La meilleure appréciation consiste à sommer les termes extra-diagonaux symétriques, ce qui fournit le tableau de pourcentages ci-dessous où les paires de mains sont cumulées et donc non ordonnées :
|
Unicolore |
Bicolore |
Tricolore |
Régulier |
|
|
Unicolore |
0,016366425 |
|||
|
Bicolore |
0,096415047 |
0,132673145 |
||
|
Tricolore |
0,011578878 |
0,029849065 |
0,001679036 |
|
|
Régulier |
0,103611855 |
0,327177422 |
0,039979229 |
0,240669899 |
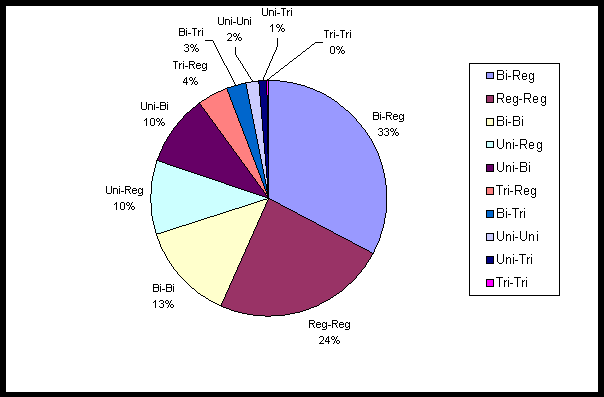
Fréquence d’une main quelconque
Chaque main dans une ligne possède un certain nombre de mains équivalentes. Nous présentons sur ce site une technique de réduction canonique qui consiste à modifier la main jusqu’à atteindre une main équivalente ayant les caractéristiques suivantes :
La main de Sud est plus longue (ou égale) que celle de Nord :
AV3 - RX872
Et non
RX872 - AV3
.
Toutes les cartes qui ne feront pas de levées sont transformées en basses cartes :
ARV9 - 875 devient ARV9 - 432
Une série d’opérations permettent les transformations de la position.
On permute tout d’abord les cartes équivalentes en mettant les plus faibles en Sud.
On substitue des basses cartes aux cartes inertes qui ne feront pas de levées :
On permute enfin les cartes fortes et faibles des deux mains, si elles sont exclusives, afin de concentrer les forces en Sud (DV2-AR43 devient 432-ARDV).
Ces opérations successives aboutissent à un résidu de
66 141 positions opposées aux 1 594 325 positions de départ. D’autres simplifications empiriques sont possibles. Si l'on ôte les mains n'ayant qu'une stratégie et les mains qui ne réussissent pour chaque nombre de levées qu'à p=0 ou à p=1, il reste 50 195 positions. L'examen du tableau (Bridge-positions.xls, téléchargeable sur ce site), montre toutefois que d'autres simplifications sont sans doute encore possibles.Le calcul de la fréquence d’une position consiste à rapporter à chacune des positions canoniques le nombre de positions qui y aboutissent. S’il est toutefois assez simple de partir d’une position quelconque pour atteindre sa position canonique, le chemin inverse est tout à fait différent car il s’agit cette fois de construire l’ensemble de toutes les positions équivalentes à la position de départ. La difficulté réside dans les interactions possibles entre différentes réductions. Donnons un exemple :
AR
VX87632
Le flanc a au maximum 4 cartes dans une main. Il y a donc 4 cartes utiles en Sud et la plus faible est le 7. Toutes les cartes inférieures sont quelconques, ce qui donne 10 combinaisons (3 cartes parmi 5 , i.e. choisies parmi 2,3,4,5,6).
Nous avons donc 15 positions de type :
AR
VX87***
Puisque AR constitue une séquence dominante en Nord, 87 seront fournis dessus et ne feront pas de levées. La hauteur de ces deux cartes est donc indifférente. Elles sont prises parmi 8 cartes (9,8,7,6,5,4,3,2) sachant que 3 ont déjà été retenues, donc parmi 5 cartes. Les combinaisons de 3 parmi 5 donnent à nouveau 10, ce qui conduit à 10 x 10 = 100 positions équivalentes. Mais ce calcul recèle en fait une erreur due au fait que certaines combinaisons sont répétées d’un calcul à l’autre et il n’y a en fait que 5 cartes à choisir (en dessous de VX) parmi 8 possibles, soit 56.
Il n’est donc pas possible de faire se succéder les expansions comme on pouvait faire se succéder les réductions.
Le logiciel ScanSuit fournit, pour chaque position analysée, sa fréquence qui est le nombre de positions équivalentes rapportées au nombre total de main d’un type donné (ces valeurs sont données dans l’article sur la programmation du maniement).